Mathematics 

Introduction to Trigonometry

Aman Gupta 246 Views 0 Comment
Spread the love

Trigonometry is a fundamental topic in mathematics, extensively used in IIT-JEE problems. It plays a crucial role in coordinate geometry, calculus, and physics. This guide will cover essential trigonometric concepts, identities, formulas, and problem-solving techniques tailored for IIT-JEE aspirants.

Systems of Angle Measurement

Sexagesimal System (Degree System)
– Angles are measured in degrees (^\circ).
– A full revolution is

    \[360^\circ\]

, and a right angle is

    \[90^\circ\]

.
– Each degree is divided into 60 minutes (‘) and each minute into 60 seconds (“”).

Circular System (Radian System)
– Angles are measured in radians.
– One full revolution equals

    \[2\pi\]

radians.
– The relationship between degrees and radians:

    \[180^\circ = \pi \text{ radians}\]

    \[1^\circ = \frac{\pi}{180} \text{ radians}\]

    \[1 \text{ radian} = \frac{180}{\pi}^\circ\]

Example: Convert

    \[60^\circ\]

to radians:

    \[60^\circ = 60 \times \frac{\pi}{180} = \frac{\pi}{3} \text{ radians}\]

Domain and Range of Trigonometric Functions

Function, Domain & Range

\sin x – (-\infty, \infty) & [-1, 1]
\cos x – (-\infty, \infty) & [-1, 1]
\tan x – x \neq (2n+1)\frac{\pi}{2}, n \in \mathbb{Z} & (-\infty, \infty)
\cot x – x \neq n\pi, n \in \mathbb{Z} & (-\infty, \infty)
\sec x – x \neq (2n+1)\frac{\pi}{2}, n \in \mathbb{Z} & (-\infty, -1] \cup [1, \infty)
\csc x – x \neq n\pi, n \in \mathbb{Z} & (-\infty, -1] \cup [1, \infty)

Example: Find the range of 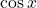\cos x if x \in [0, \pi].

From the table above, \cos x has a range of [-1,1].
In [0, \pi], \cos x decreases from 1 to -1.
Thus, the range of \cos x in [0, \pi] is [-1,1].

Trigonometric Ratios of Some Angles

Angle, \sin x ; \cos x ; \tan x ; \csc x ; \sec x ; \cot x

0^\circ – 0 ; 1 ; 0 ; \infty ; 1 ; \infty
15^\circ – 0.2588 ; 0.9659 ; 0.2679 ; 3.8637 ; 1.0353 ; 3.7321
18^\circ – 0.309 ; 0.9511 ; 0.3249 ; 3.236 ; 1.0515 ; 3.0777
45^\circ – \frac{\sqrt{2}}{2} ; \frac{\sqrt{2}}{2} ; 1 ; \sqrt{2} ; \sqrt{2} ; 1
80^\circ – 0.9848 ; 0.1736 ; 5.6713 ; 1.0154 ; 5.7588 ; 0.1763
90^\circ – 1 & 0 ; \infty ; 1 ; \infty ; 0

Example: Find \tan 45^\circ.

    \[ \tan 45^\circ = \frac{\sin 45^\circ}{\cos 45^\circ} = \frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}} = 1 \]

Previous Years’ IIT-JEE Solved Questions

Question 1 (JEE 2020): Find the general solution for \sin x = \frac{1}{2}.

Solution:
\sin x = \frac{1}{2} \Rightarrow x = n\pi + (-1)^n \frac{\pi}{6}, n \in \mathbb{Z}

Question 2 (JEE 2018): Evaluate \tan^{-1} \left( \frac{\sin x}{1 + \cos x} \right).

Solution:

Using the identity:
\tan^{-1} \left( \frac{\sin x}{1 + \cos x} \right) = \frac{x}{2}
Thus,
\tan^{-1} \left( \frac{\sin x}{1 + \cos x} \right) = \frac{x}{2}

Conclusion

This guide provides an introduction to trigonometry tailored for IIT-JEE preparation. Mastering these concepts, formulas, and problem-solving techniques will significantly enhance your ability to tackle JEE-level problems efficiently. Practice is key to excelling in trigonometry, so keep solving problems regularly!

You May Also Like

Conic Sections - Tangents, Normals, Locus Problems

Conic Sections – Tangents, Normals, Locus Problems

Aman Gupta 0

Leave a Reply